Unicomplex numbers are just a way express floating point numbers in a way that gives them an additional precision clue. A the time is this writing, it has no practical applications beyond the study of numbers and their representation in computer systems.
UPDATE: I recently (2024-03-03) found out about gmpy2 that may or may not adress some of the issues I mention here ; FYI I have not tested gmpy2 or compared it to my results in any way.
I related them to complex numbers because i² = -1, and mutliplying a number with its opposite inverse1 (ie. -1/n) gives (or at least should) the result -1 (which, conveniently enough, is the square of the complex number i). In this regard, the complex number i is just a number that equals it’s opposite inverse.
One idea behind this is to make all operations twice, in a way to get a range for the result ; this is no stranger than the fact that there is no exact floating point binary representation of the infamous 0.1 (such numbers will always be approximated within a certain range) and this is due to the way in which they are expressed and the granularity resulting from this.
As a result a small script was written and I will briefly analyze the results.
Script
def uni(n):
""" converts a number to its unicomplex form """
c = n*(-1/n)
if c != -1:
print("warning, significant error in uni()")
return ( n, -1/n, c )
def p(n):
""" prints a number with most available decimals """
if type(n) is float or type(n) is int:
n = (n,)
return ' '.join(["{:0.62f}".format(m) for m in n])
N = uni(.1)
M = uni(.3)
def add(a,b):
""" a,b must be uni() """
r = [0,0,0]
r[0] = a[0]+b[0]
r[1] = -1/(-(a[1]+b[1])/(a[1]*b[1]))
#p(-1/r[1])
#p(r[0]-r[1])
r[2] = -(abs(r[0]-r[1])+a[2]+b[2])
#p(r)
return r
print("Starting with two numbers, 0.1 and 0.3")
print(p(N))
print(p(M))
print()
print("We add these, which in theory is 0.4")
q = add(N,M)
print(p(q))
print()
print("Now we recursively add our theoretical 0.4 to itself, and take this value for the next addition")
for i in range(64):
q = add(q,q)
print(i, p(q))
Result and short analysis
The image below is the result of 64 successive additions of the value 0.4 to itself, taking that result and adding it to itself, and so on.
First, it can be noted that the opposite inverse of our computed 0.4 value is actually more accurate than the value we’re actually expecting (0.40000something) ; the same can be said for 0.1.
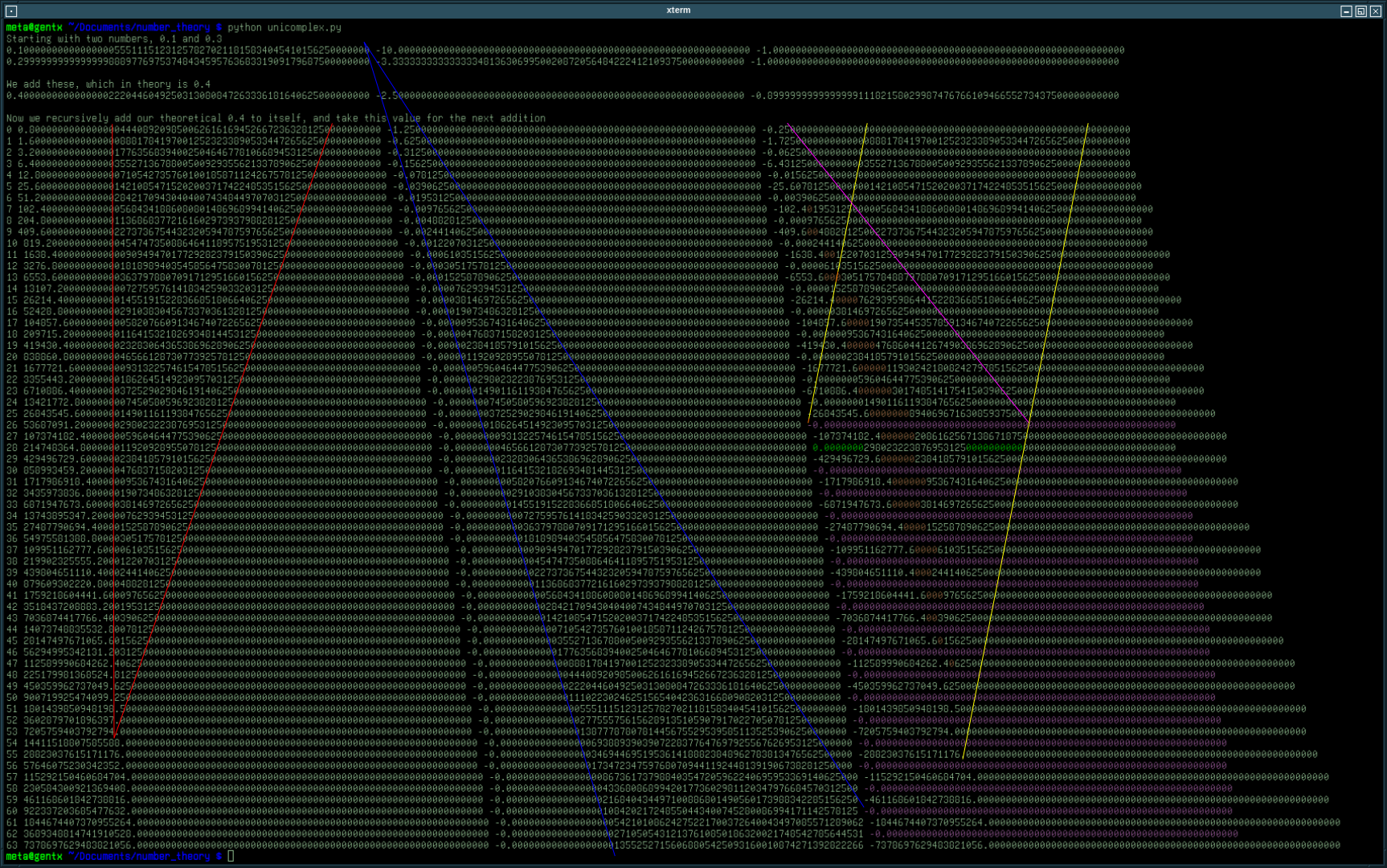
We can notice some patterns, which have been highlighted for the sake of this demonstration.
- the red triangle delimits some garbage decimals in the number we are expecting : these are decimals which contain an error that gets compressed as it shifts towards the integer as we iterate (the error gets more and more significant relative to the unit)
- the blue triangle delimits the siginificant figures of 1/n and obvioulsy expands while shifting to the right as n increases ; when the right side of the triangle hits the right edge of the number we are definitely loosing some data, and when its left side hits the right edge of the number, well it clearly makes no sense to consider the number as a floating point number because its inverse will always be zero - sort of like the inverse of infinity so relative to the range covered by floating point numbers, we have basically reached infinity (and any result must be regarded with high suspicion)
- the purple line shows what I call the expected error propagation : we know we’re dealing with floating point numbers, therefore there is an error
- the yellow parallel lines in the error component basically shows how unpredicitible the error is : you may notice that in this case, there are oscillations every two iterations, and that shifts towards the integer component of the number
When the red triangle meets the decimal point, we are basically off by one unit (at i = 53, we should have 7205759403792793.6). This is also, with little to no surprise, where the rightmost yellow line hits the decimal point.
When the purple line meets the rightmost yellow line, the error component starts oscillating between -0.0 (I bet a lot of math teachers would get very upset by this negative zero value) and large negative values (they may look as they are integers, but they are still floating point numbers) ; at this point the error has become significant and anyone concerned with precision should really consider using an abacus.
We can also notice that the error componenent contains, every second iteration once the expected and unpredicitible errors start interfering and before the situation really degenerates, a series of zeroes (highlighted in orange) somewhere in the middle of its significant digits ; that series is the longest around the point we mentionned last, just before what I call the friend zone (anything can happenthere but its usually disappointing for everyone), where some zeroes are highlighted in green and we don’t quite have -0.0 where we would expect it.
It is interesting to note how the error component behaves as iterations continue:
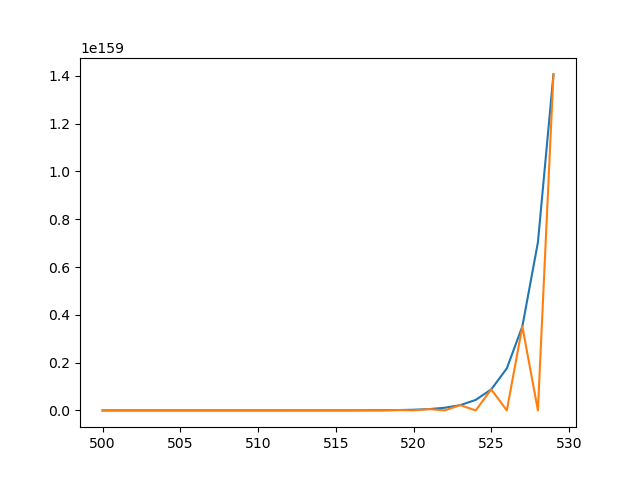
In the above graph (the left side was truncated) we plot the number (in blue) and the error component (negated, in orange) : the error keeps on oscillating between -0.0 and a little more than -n until we get a ZeroDivisionError in our little add() function2. From this, it seems obvious that the numbers we are dealing with are of very relative use since the error averages to half the value of these numbers, way before our computer complains that something is wrong : it has actually run out of digits after about seven sums only.
Conclusion
Errors accumulate very fast, and start interfering with the expected results faster than one could imagine.
Don’t use floats, especially not floating point operations. Or yes, you can, but really know that you’re dealing with what is probably one of the most evil things computer science has come up with. In all cases, definitely favor integers or an algebraic approach3.
As for me, I believe there’s a little more to look at there and I might very well give it some more thought in the future, so be sure to come back some other time.