The Sudokube is a 9⨯9⨯9 Rubik’s Cube with a particularity : instead of displaying a different color for each face, it features 6 unsolved Sudoku Grids! Sudokube is hard not only because it’s a fairly large Rubik’s Cube, but mostly because the player must solve each Sudoku grid before being able to solve the Rubik’s Cube ; this is most tricky since - when the Rubik’s Cube is shuffled - there can be a lot of possible arrangements of the cubelets.

However, we also know there are only 6'670'903'752'021'072'936'960 different Sudoku grids¹, so it has become obvious that we have some collisions ; in theory, it should therefore be possible to have every possible Sudoku grid on our cube. Does it mean we’ve failed?

The question

• What is the minimal number of clues needed to ensure a unique solution? How many such cubes are there?
• How does the cube behave when some symbols can have different apparent orientations (such as the 6 and 9)? Can we make a cube that requires no context (ie. a line at the bottom of the figure) added?

10:54 < isabella> the only piece that can be rotated in place is the very centre of each 9x9 face
10:55 < isabella> and it can only be rotated by 180degrees if the rest of the cube is solved
10:55 < isabella> same applies for all nxn cubes with odd n, only the very centre of each faces

• What other fun cubes can we come up with? Say we have not 9 different symbols (they don’t need to be numbers from 1 to 9) but 12 (always 9 unique symbols per Sudoku grid), can we come up with different arrangements that also have a unique solution?

Solving the problem

Above is a deconstruction of a 9-Rubik’s Cube ; let’s look at its properties :

• The ‘8’ symbols at the center never move relative to each other ; on a solved Rubik’s cube, they can be rotated 180°
• If we only take the letters into account, the cube is always solved, no matter what moves are applied to it.
• If we take the letters and colors into account, we notice that - regardless of the orientation - each letter can be at 4 different places but that is not valid for the edge and corner pieces (unless we reduce the number of colors)
• If we only take the letters and orientation (the twisted arrow symbol), without colors, each symbol has 6 valid locations
• The above cube (with colors, letters and orientation) has only one unique solution ; however it’s a bit too obvious and trivial so we want to add some blanks

This leads us to some conclusions:

• Since the center piece can be rotated by 180°, the symbol it holds must not be symmetrical (‘8’ is not great ; there should be only one ‘6’ or ‘9’ on the cube at this center position and it’s desirable - makes it confusing and harder to solve - to have at least one ‘6’ or one ‘9’ there)
• We want at least one symbol on every box of the color-less plane (flat grid) ; this may not be enough to make the cube “perfect” (only one solution) but helps make it a little bit trickier. A single unknown value is OK.
• We don’t want the same symbol to appear twice on the quarter-plane (the small 1-4 numbers)
• It is undesirable to have two same grids (once solved) on different faces of the cube

Taking the minimal-clue Sudoku puzzles which have 17 of them², it becomes obvious we will have a minimum of 102 clues total, leaving 384 blank boxes. Now, can we still have a unique solution (without adding additional clues such as orientation) in this case? It seems not.

Result

After a few hours of coding, I came up with a script that generates some stickers that can be added to a 9x9x9 cube (ideally monochrome or previously scrambled) ; I decided to not go through the hassle of giving the Sudokube a unique solution (there may be some admissible permutations on blanks) but since a regular Rubik’s Cube also has many solutions, I figured it’s totally OK : these permutations are not the same type that a standard Rubik’s Cube allows so this will get you out of your comfort zone either way. Otherwise, no permutations are allowed on cubelets with a symbol.

There are a few variants, of which my two favorites are displayed below:

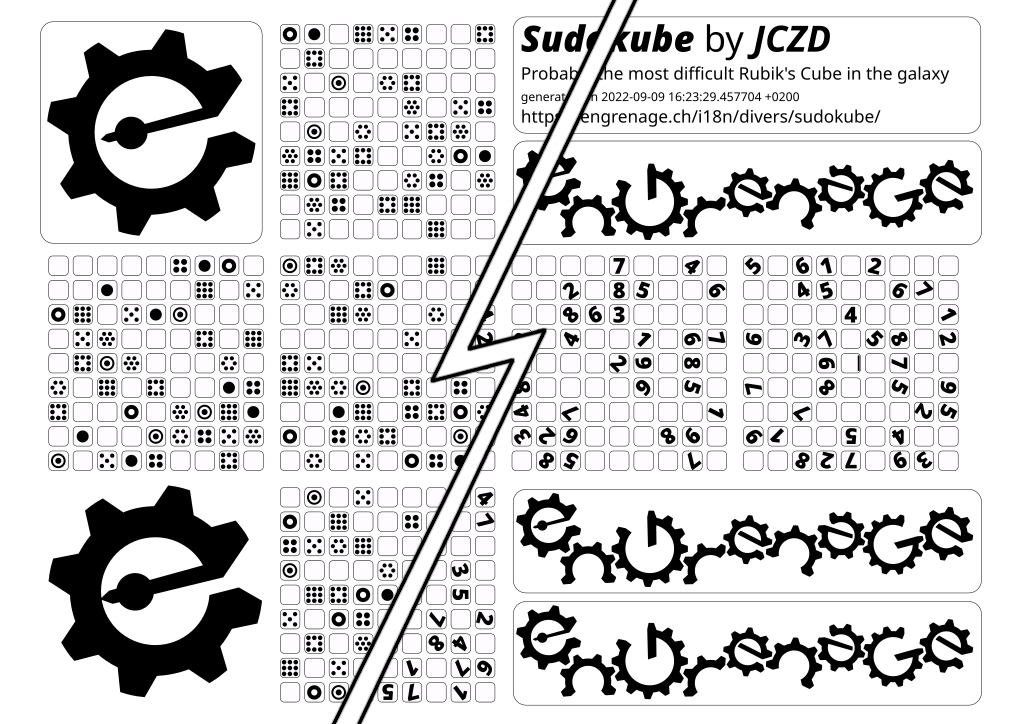
You can contact us to get your own set of stickers or even a cube with the stickers on it (and to make it extra difficult, it will have been scrambled for you) ; your Sudokube s very likely to be unique and will be signed (the top-right sticker acts as a certificate of authenticity).

Alternatives

Small Sudokube

A much simpler version of the Sudokube is one where the Sudoku grid is laid out on a 3⨯3⨯3 Rubik’s Cube. Very boring, but good for demonstration purposes. Another one is base-4-based but from the maths involved, it seems it is not possible to have any blank squares so it’s quite boring too. It’s just a little more obscure (and less permissive) than a standard Rubik’s Cube : there are too many possible permutations and this makes it boring (again) ; taking into account the equivalence of symbols, it seems there really aren’t many distinct solutions available (how many? this is yet to figure out).

Here is a full example, taking into account 45° diagonals:

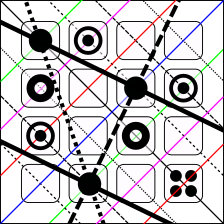
• there are 3 possible possible positions for the first symbol
• there are 2 possible possible for the second symbol, these will exclude all other
• there is only one possible position for the third symbol, these will exclude all other
• the 4th symbol can be put into any of the remaining 8 positions, thus excluding the 7 positios left over
• taking into account a further diagonal is equivalent to a horizontal or vertical line

It becomes obvious when we consider the semi-diagonals shown in thick lines ; there are some collisions ; this relates to how Cantor was wrong but is beyond the scope of the current article.

This yields some very interesting conclusions on 3-D space and number- or group-theory, but this is also beyond the scope of this document. More on this later.

Rubichess

The Rubichess is 8⨯8⨯8 Rubik’s Cube where each face features a game of chess that was started ; since there are only a finite number of possible arrangements on the chess board (one cannot randomly set the pieces on the board and expect there will be a valid set of moves that will put all parts in this position) it should be possible to find a set of six chess games that yield a unique, valid solution for all faces of the Rubik’s Cube.

Simpler variants of the Rubichess can sit on 4⨯4⨯4 or even 2⨯2⨯2 cubes.

RubiGo

Same like above, only it’s a 19⨯19⨯19 cube, featuring games of Go. This one is massively hard, whether it is to construct or to solve. At the moment, I’m not sure this is even possible at all, mainly because the stones have no orientation.

References

• More types of Sudoku grids: 6 Different Types of Sudoku Puzzles You Should Try